1. the factoring method
Solve in positive integers 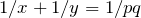 , where
, where 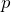 and
and 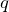 are prime.
are prime.
Solution: , so
, so 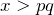 .
.
Solution:
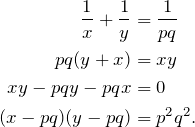
Considering the positive divisors of ![]() we obtain:
we obtain:
![Rendered by QuickLaTeX.com \[ \begin{cases} x-pq=1\\ y -pq=p^2q^2 \\ \end{cases} \quad \begin{cases} x-pq=p\\ y -pq=pq^2 \\ \end{cases} \quad \begin{cases} x-pq=q\\ y -pq=p^2q \\ \end{cases} \quad \begin{cases} x-pq=p^2\\ y -pq=q^2 \end{cases} \]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-cf48acb2b3c4f13bd934fbc667edd966_l3.png)
yielding the solutions (writing ![]() ):
):
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
and their equivalents with ![]() and
and ![]() swapped. And the special case:
swapped. And the special case:
![Rendered by QuickLaTeX.com \[ \begin{cases} x-pq=p^2\\ y -pq=q^2 \end{cases} \]](https://www.adamponting.com/wp-content/ql-cache/quicklatex.com-e69c44cc9023b3f3debcf2da7b06420d_l3.png)
with the solution ![]() , i.e. 9 solutions in all.
, i.e. 9 solutions in all.
![]()
where ![]() , has
, has ![]() solutions in positive integers.
solutions in positive integers.
The equation is equivalent to ![]() and
and ![]() has
has ![]() positive divisors.
positive divisors.
(to be continued)
further reading
Andreescu, Andrica, Cucurezeanu – An Introduction to Diophantine Equations