1. Assume the general form of the answer
2. Impose the condition that the induction be true for ![]() (or other convenient value)
(or other convenient value)
3. Impose the induction condition that the step from ![]() to
to ![]() be true.
be true.
4. From 2 and 3, determine the unknown coefficients.
Example. Find the formula for ![]()
Since ![]() and
and ![]() , it seems the closed form of
, it seems the closed form of ![]() will be a polynomial of degree
will be a polynomial of degree ![]() . (Educated guess.)
. (Educated guess.)
Step 1. Write a polynomial of degree 4, with 5 undetermined coefficients:
![]()
Step 2. With ![]() , i.e. no terms, we get
, i.e. no terms, we get ![]() .
.
Step 3. Apply the induction step from ![]() to
to ![]() : add
: add ![]() to both sides, and substitute
to both sides, and substitute ![]() for
for ![]() .
.
![]()
If the induction is to work, the RHS must be equal to ![]() .
.
Step 4. Equate the two expressions:
![]()
Rearrange the LHS. Use binomial expansion, and arrange coefficients to match the RHS powers of ![]() :
:
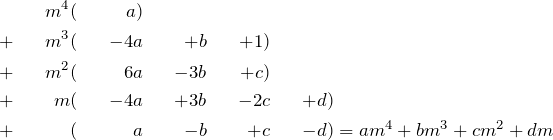
Equating the coefficients of ![]() , we get
, we get ![]() .
.
Equating the coefficients of ![]() , we have
, we have ![]() .
.
Equating the coefficients of ![]() , we have
, we have ![]() .
.
And from ![]() .
.
Now the coefficients are determined, and the sought formula is:
![]()