I came across this page On de Bruijn Grids and Tilings years ago, maybe 10, and always thought it was very cool. Basically, draw 5 groups of equally-spaced parallel lines, 72 from each other, and rhombuses drawn on the points of intersection can be arranged into a tiling – Penrose’s quasi-5-fold-symmetry tiling using 2 rhombuses.

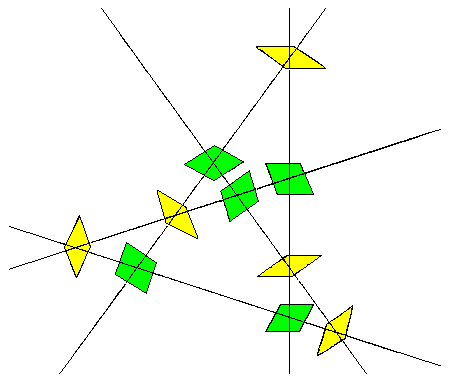
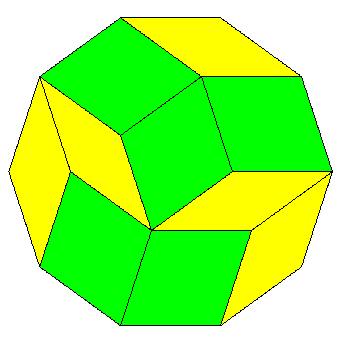
They also give a version with lines in 7 directions, using 3 rhombuses.

Last week I wrote a program to construct tilings, given the lines. I tried it with de Bruijn’s pentagrids and multigrids, and soon realized it works with lines in any direction, even with lines of random angle and position. So far I haven’t found any mention of people using de Bruijn’s method with anything but parallel, evenly-spaced groups of lines. Martin Gardner wrote about the Penrose tiling in the mid-1970s, with contributions from Conway, and later about de Bruijn’s methods to construct them, which date from the early 80s. It’s discussed in Branko and Grunbaum’s book on tilings from the 80s. So I’m not sure what to call it – mostly it’s called de Bruijn’s multigrid method, but the ‘grid’ means evenly-spaced lines, and this isn’t that. “de Bruijn tilings” for now, I guess – as far as I know, the idea of making tilings from the crossings of straight lines is his.

Some examples of what I’ve thought of trying so far:

3-fold symmetry

quasi-5-fold symmetry

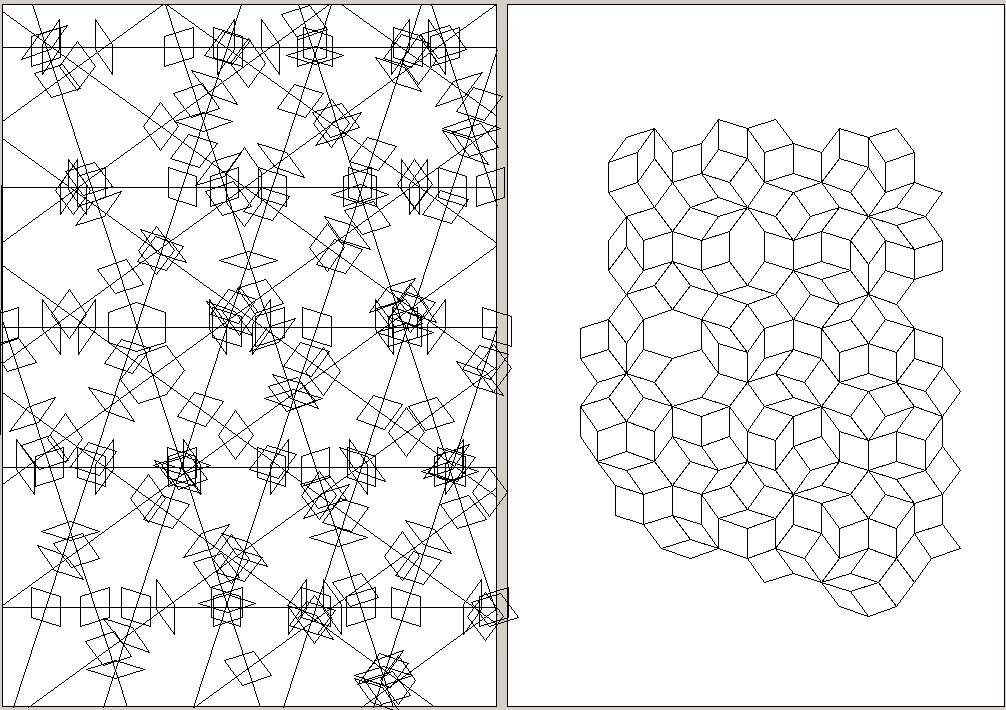
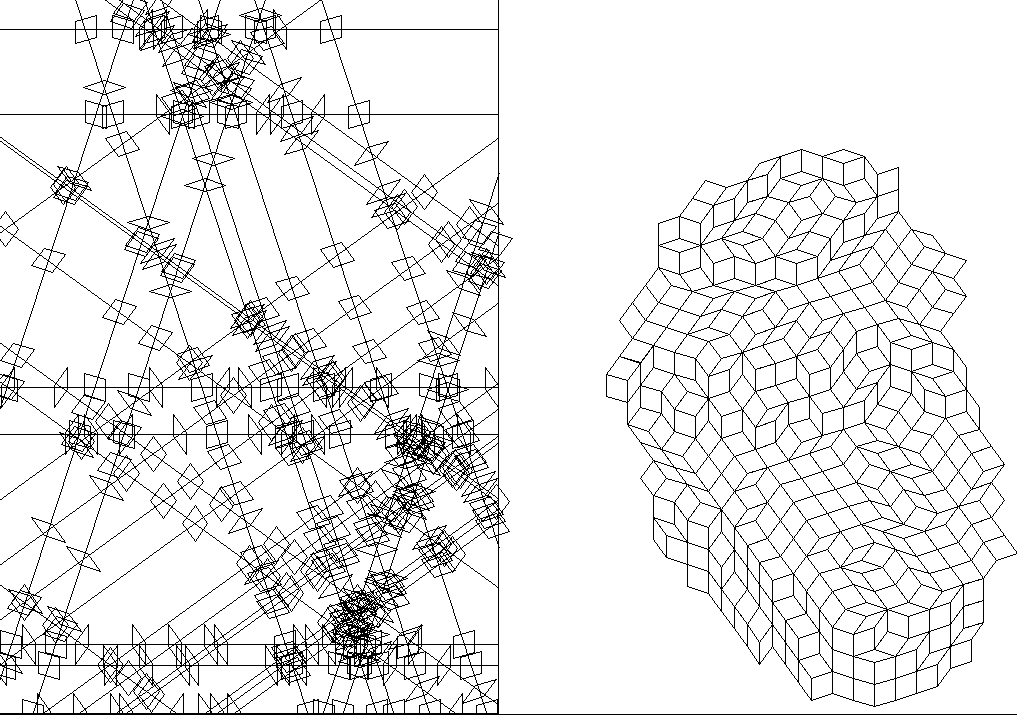
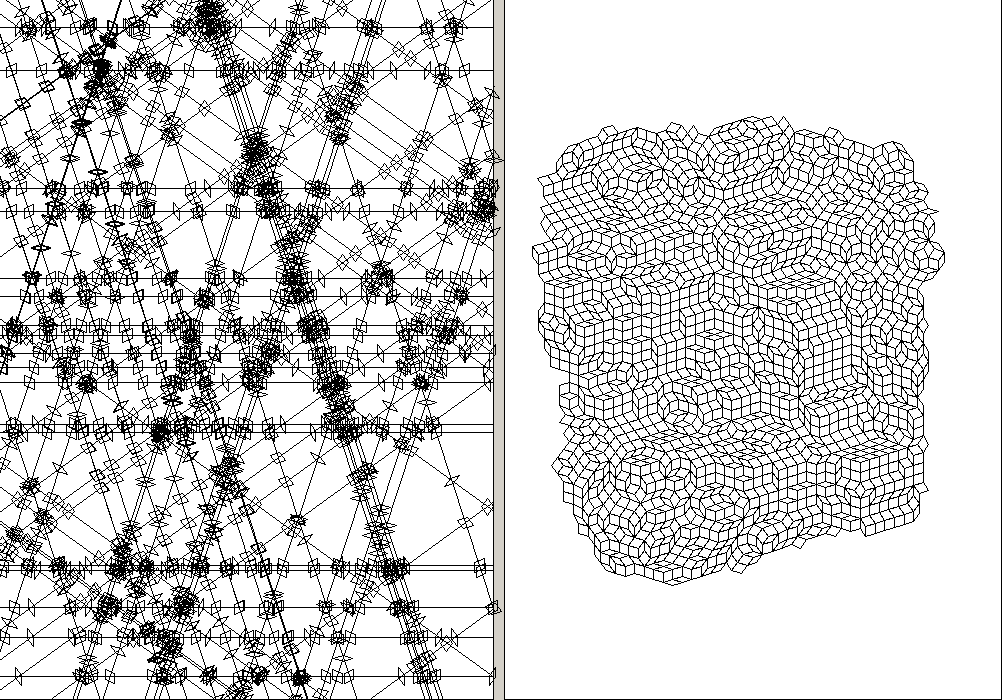
5-fold symmetry, 80 lines

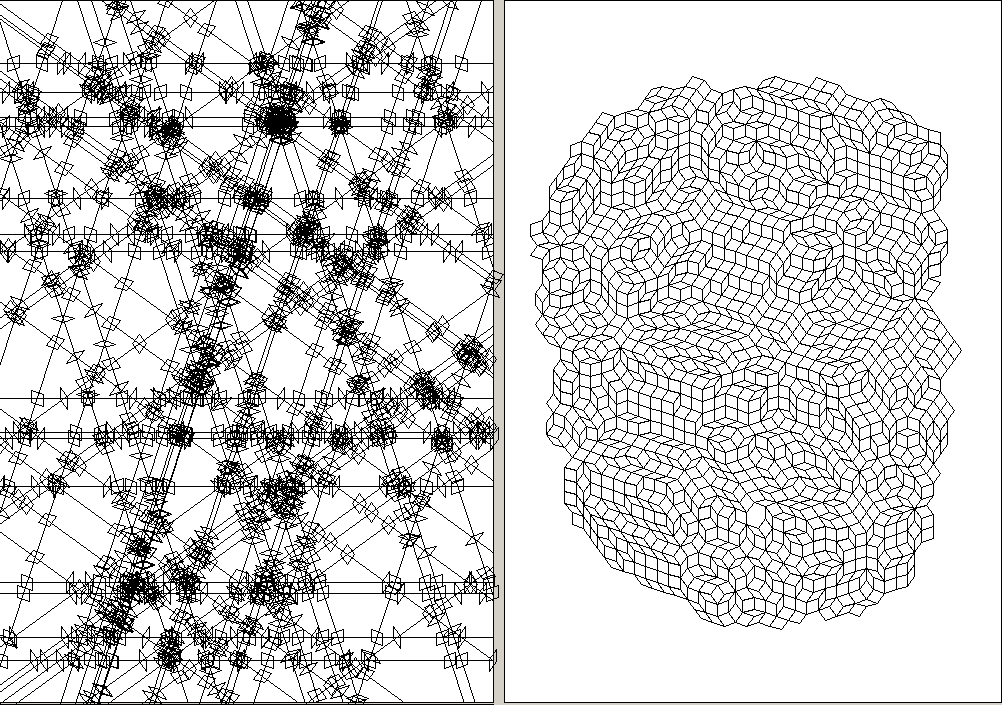
7-fold symmetry

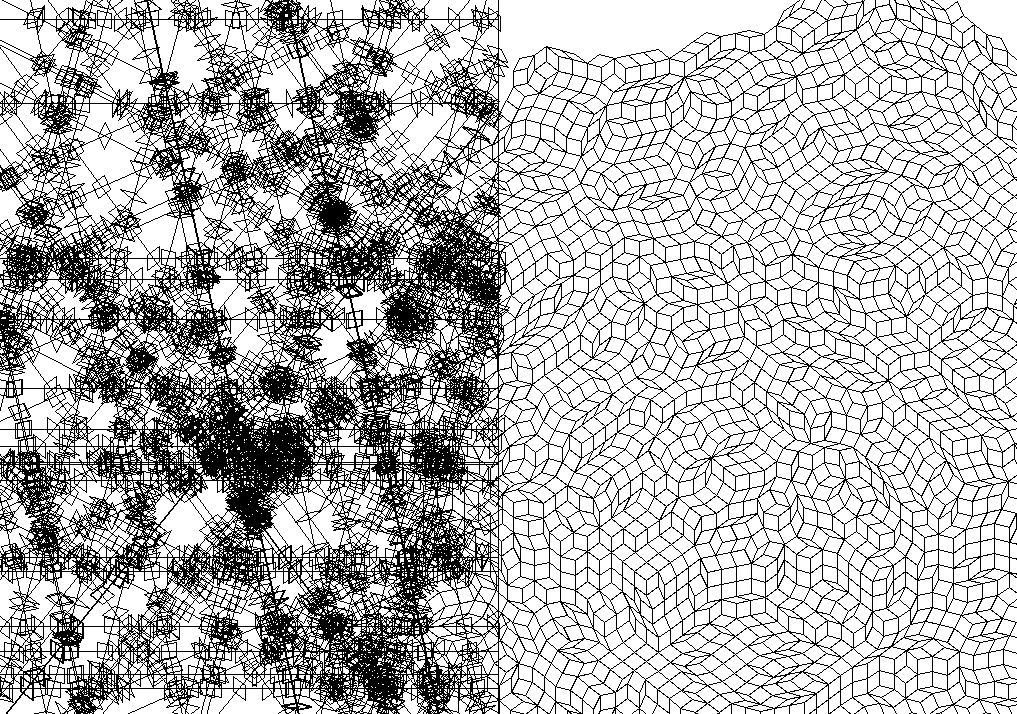
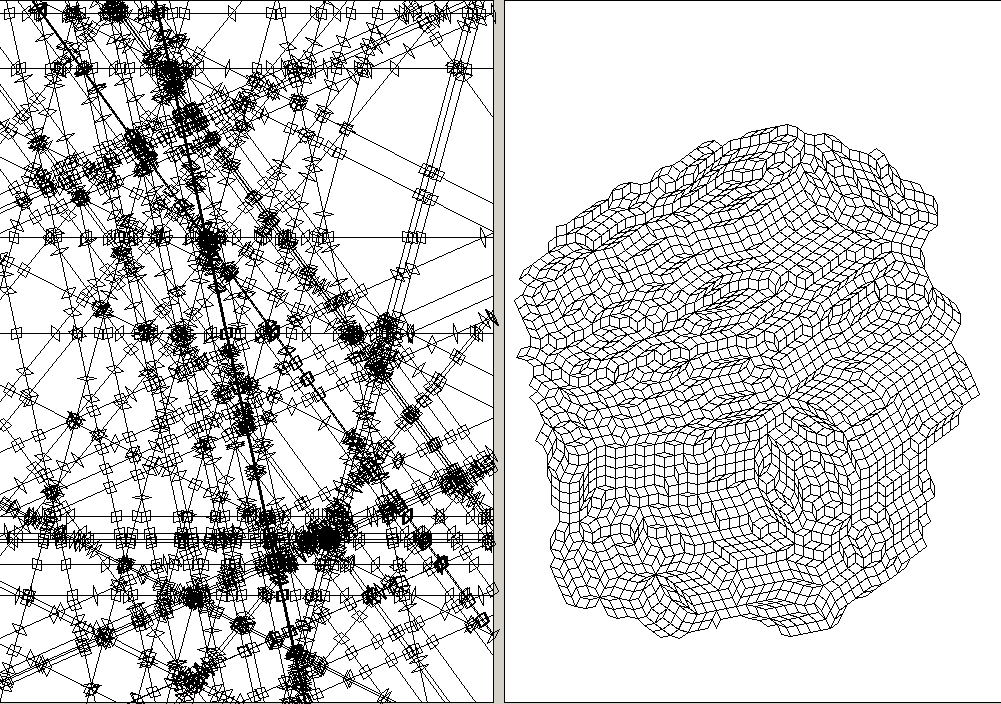
7-fold symmetry with 110 lines (3307 shapes)

8-fold

9-fold

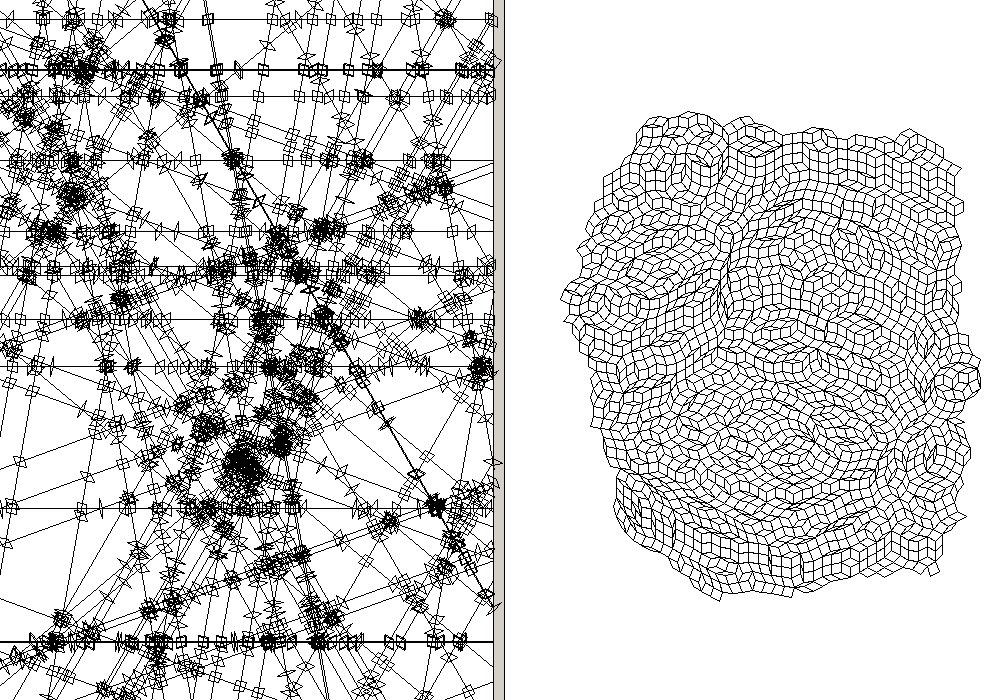
11-fold

13-fold

41-fold

Grid, using 3 random angles

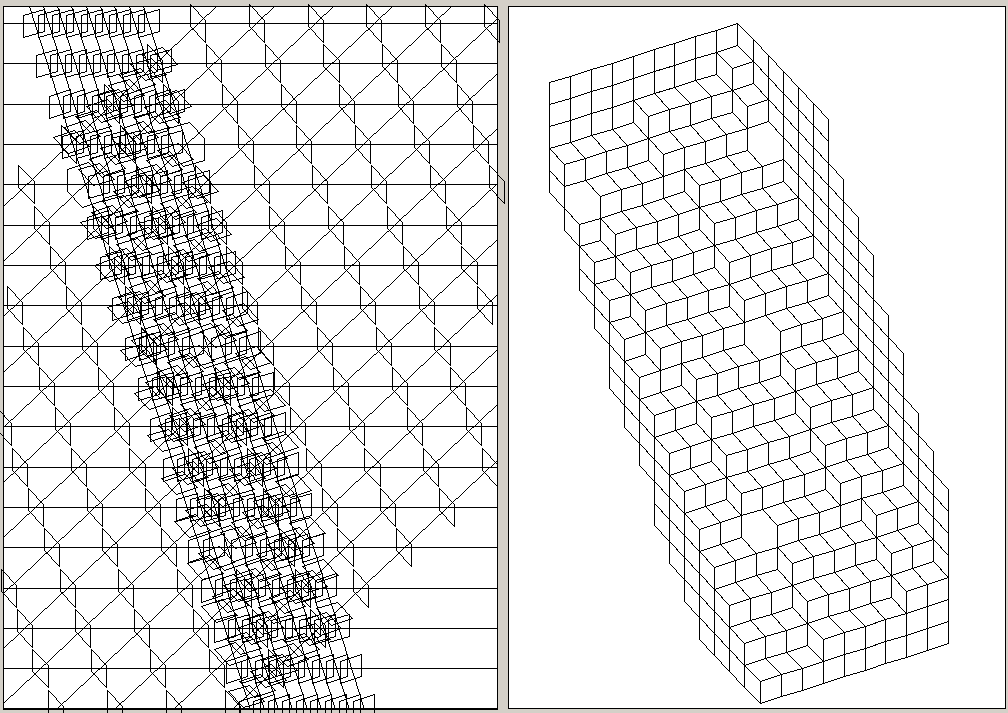
non-parallel lines

random lines

20 random lines

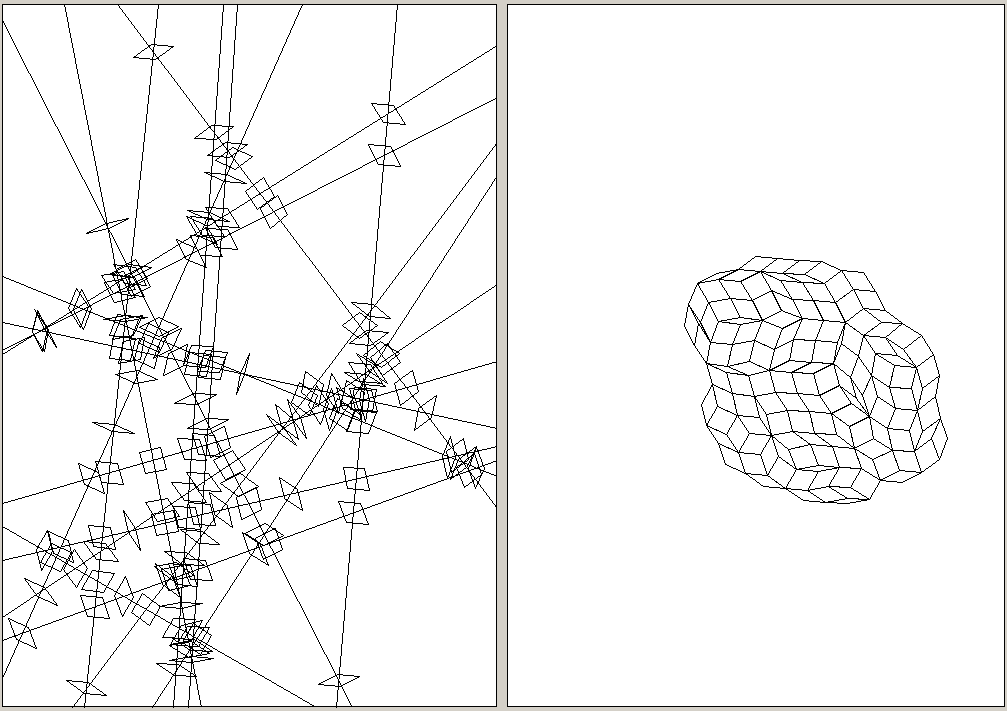
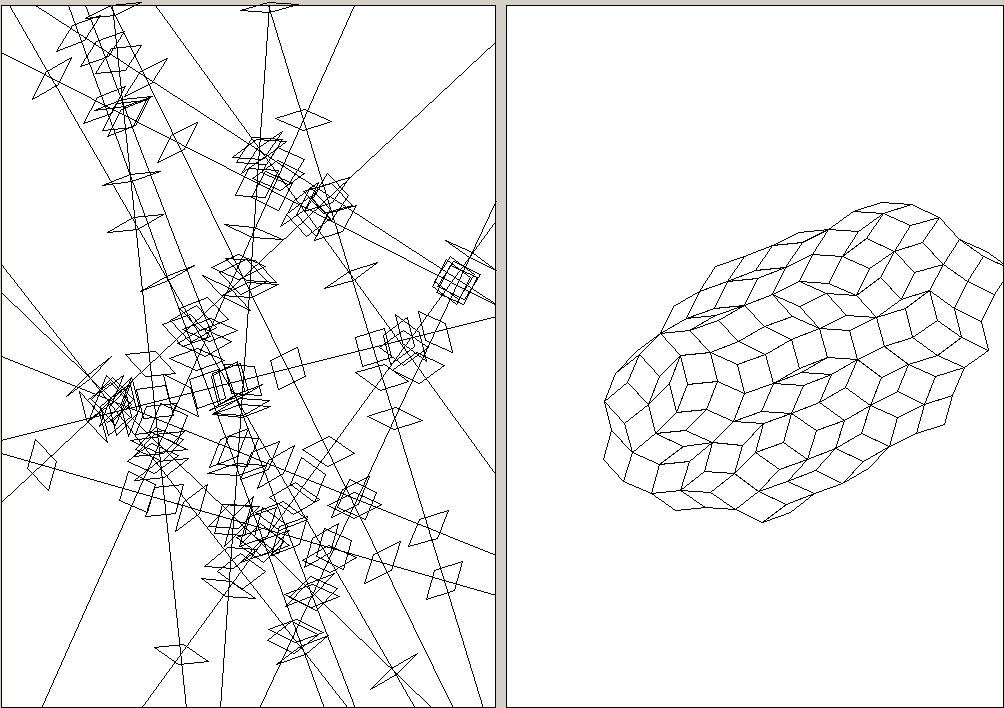
30 random lines

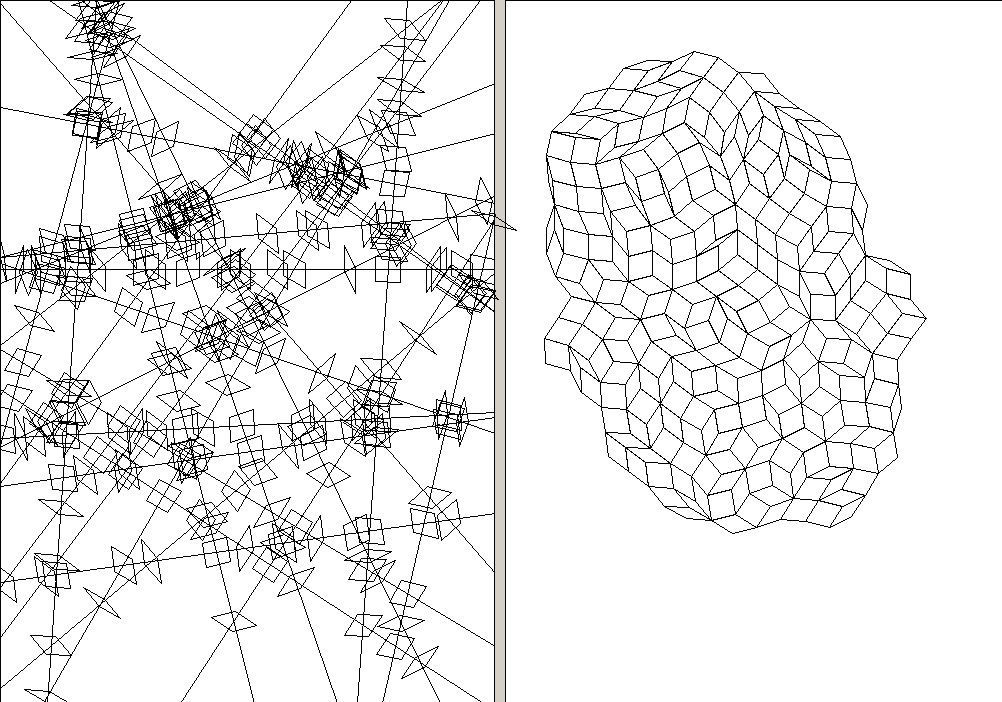
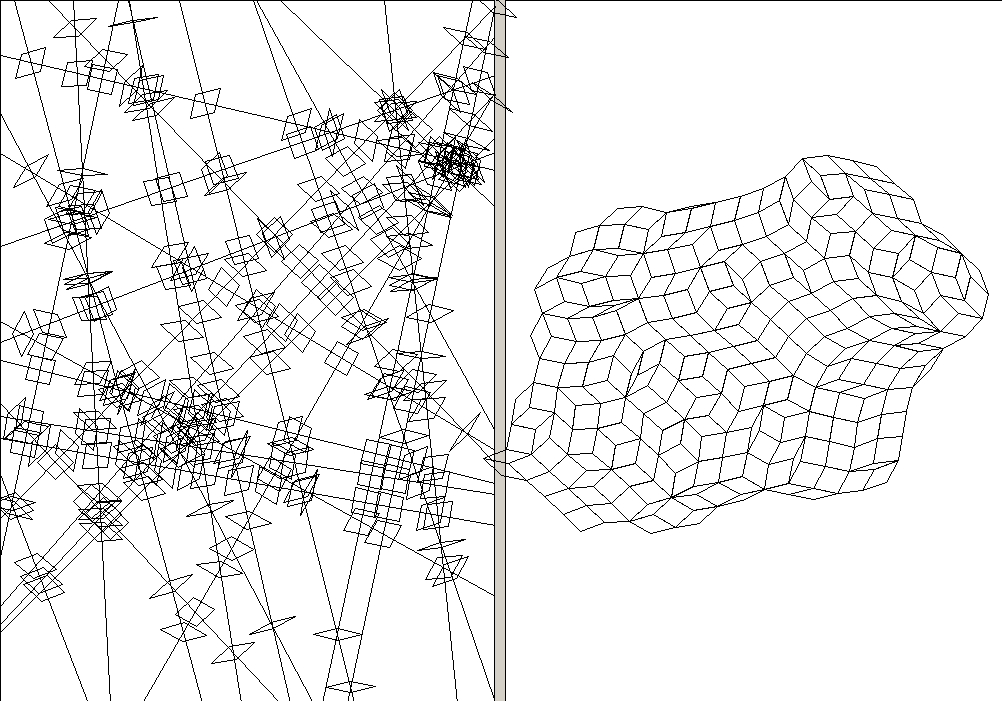
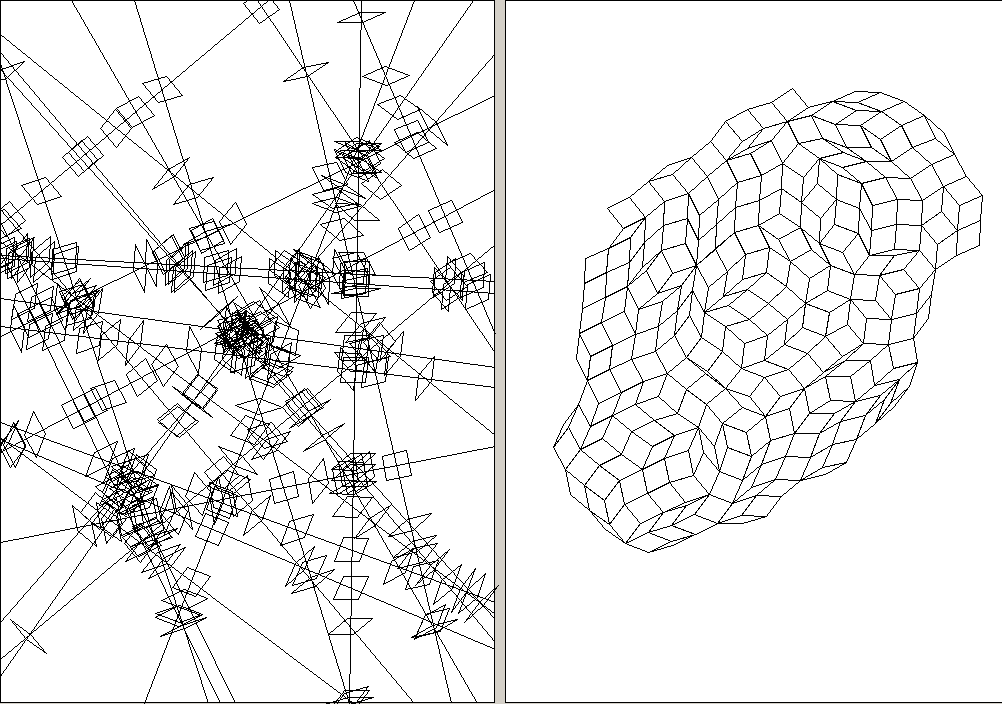
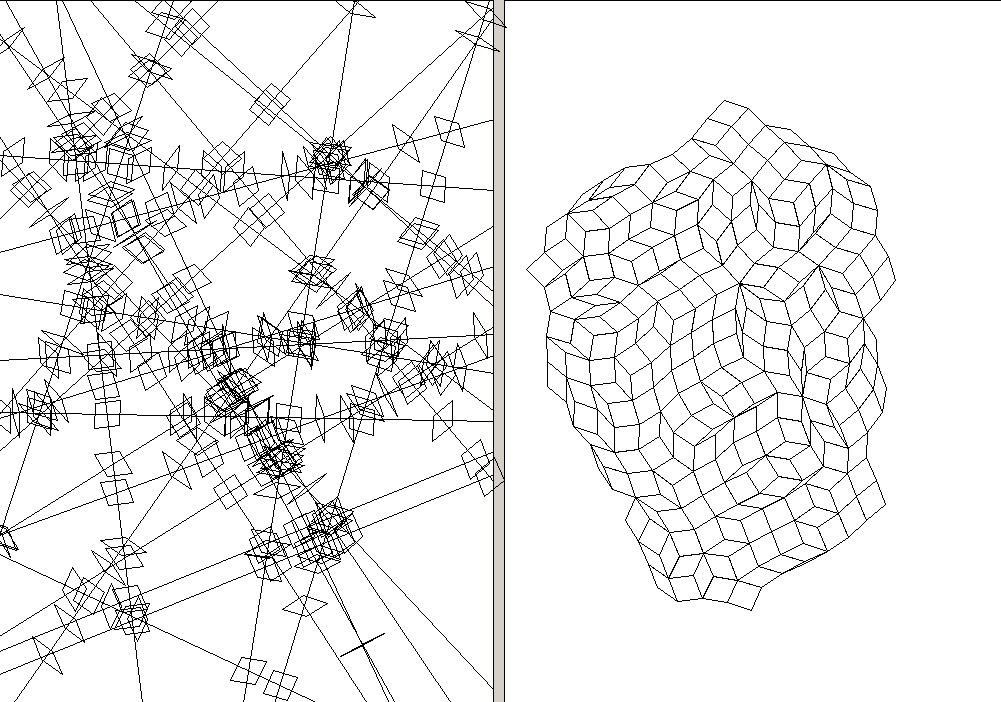
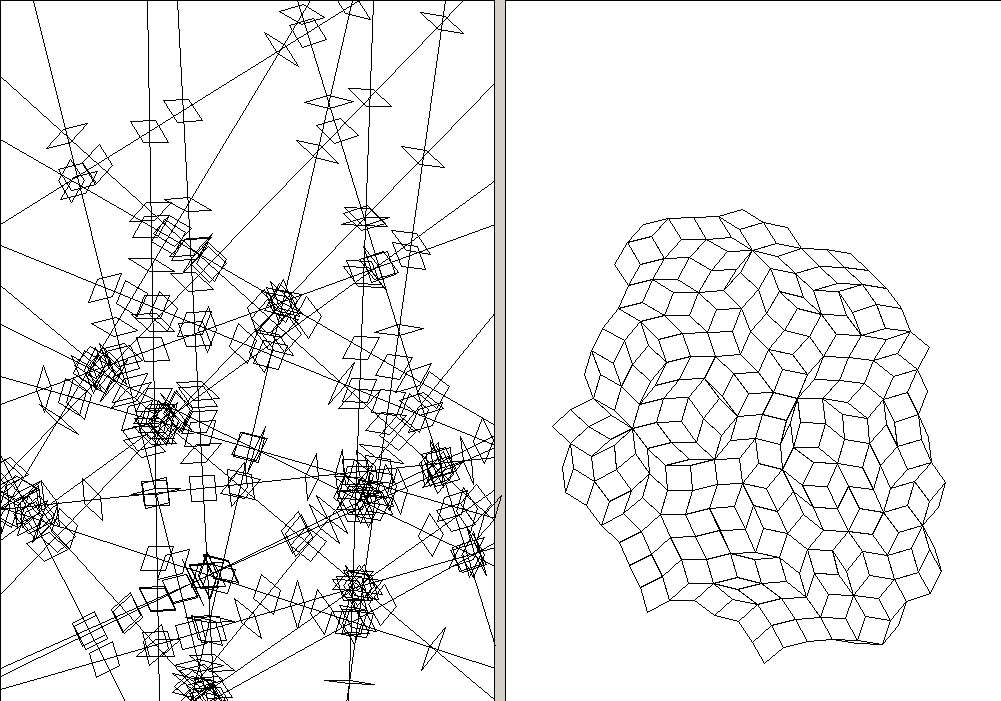
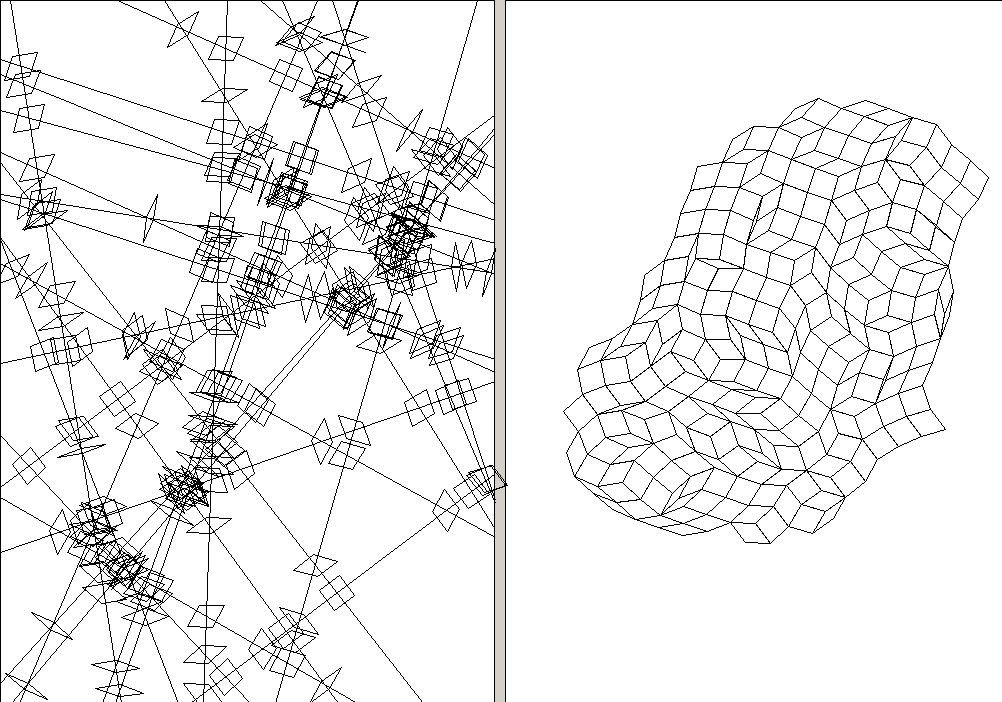
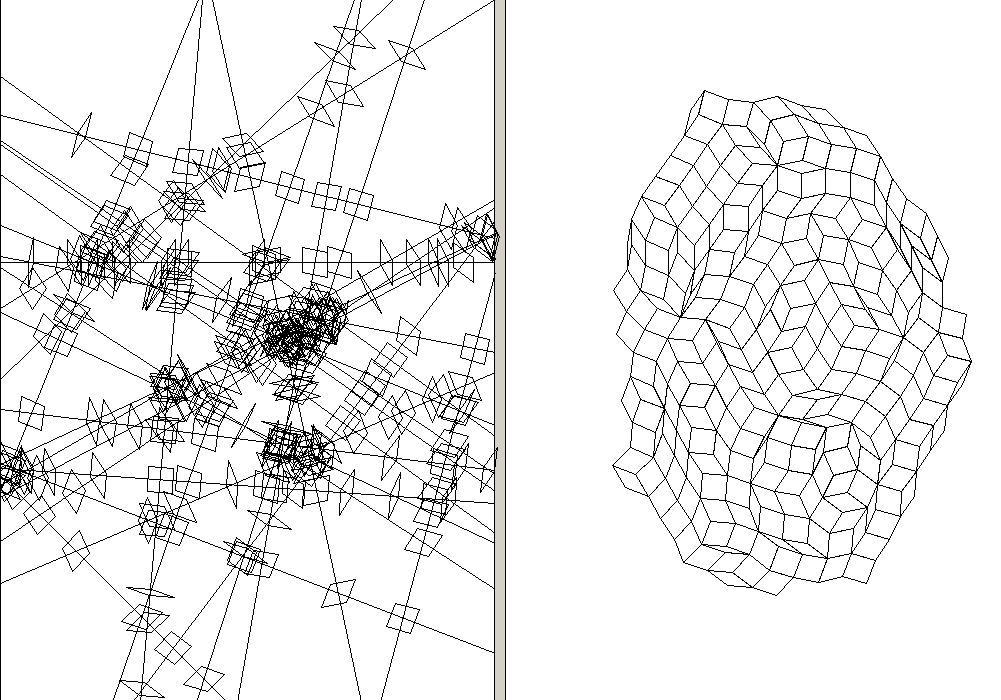
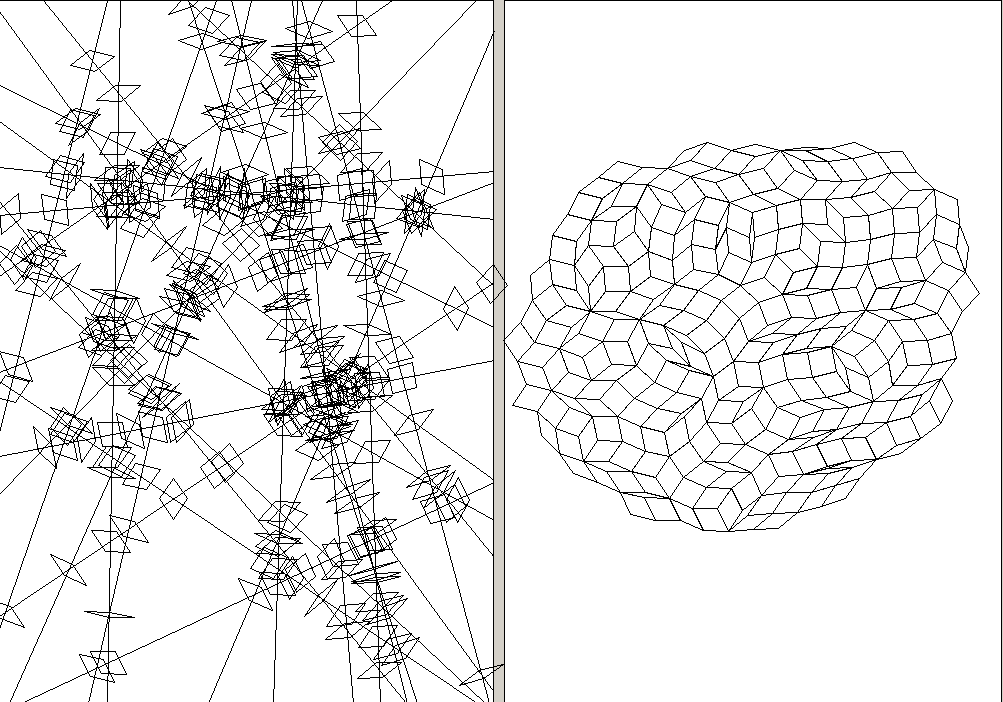
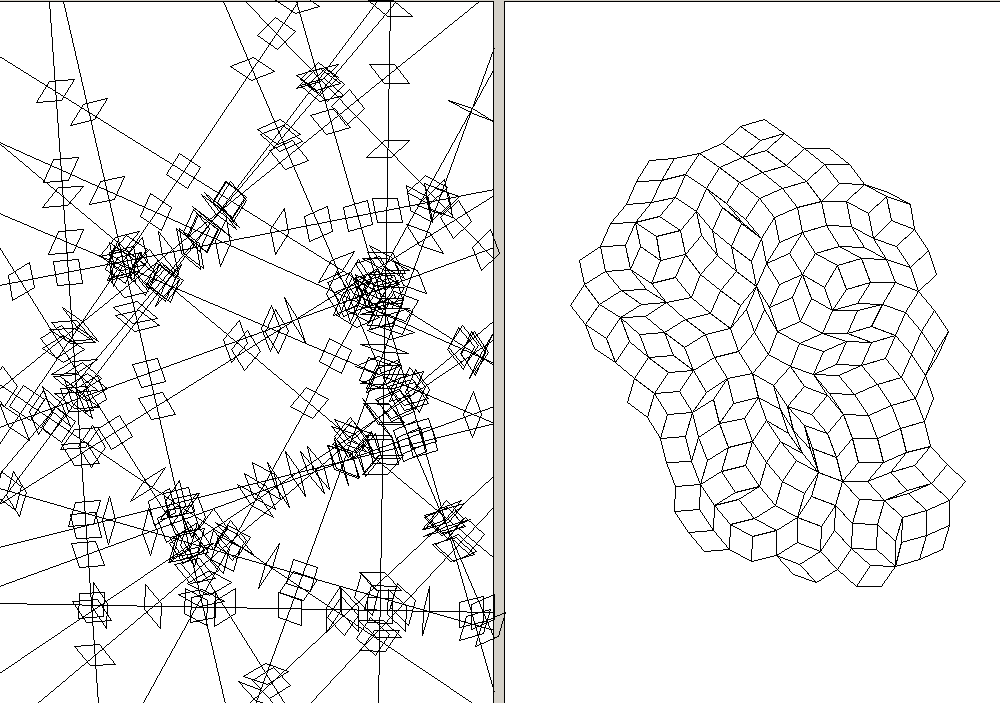
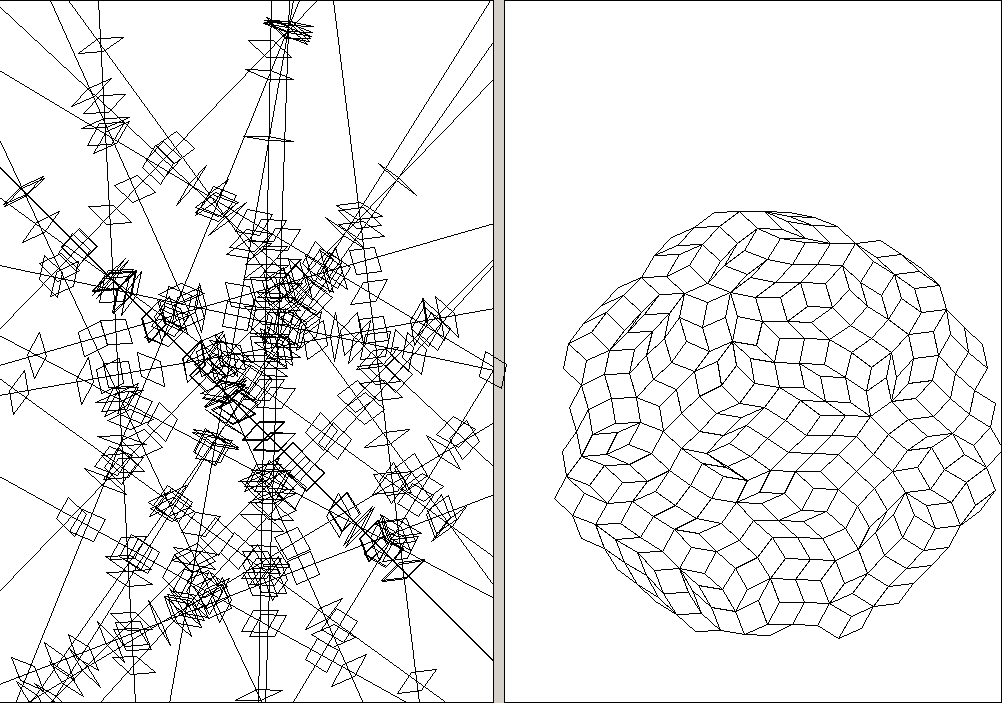
50 random lines

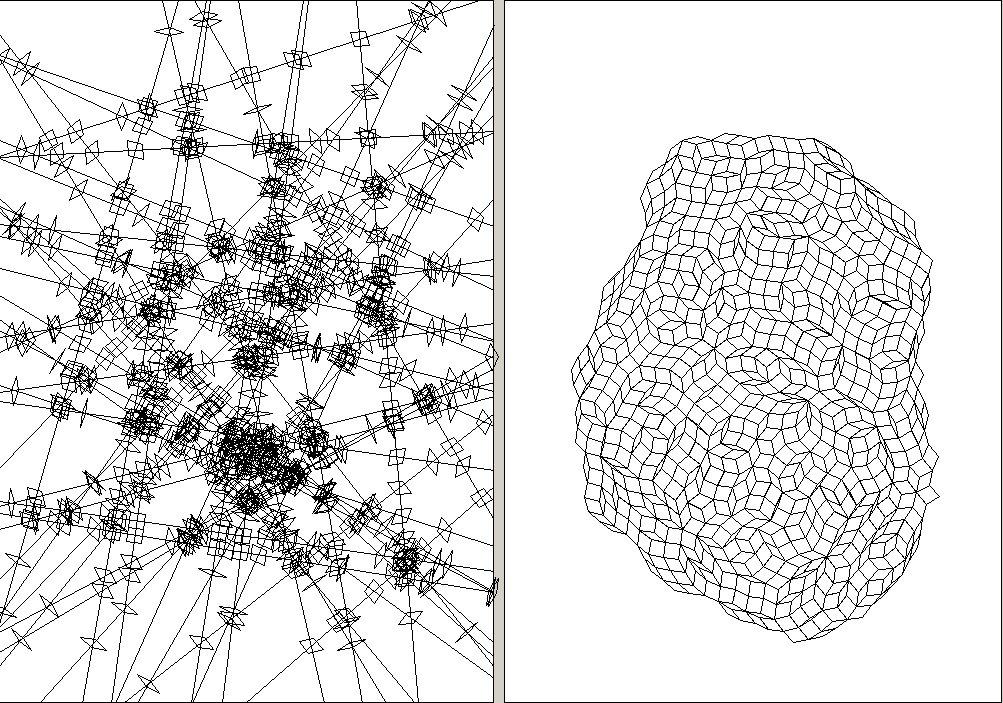
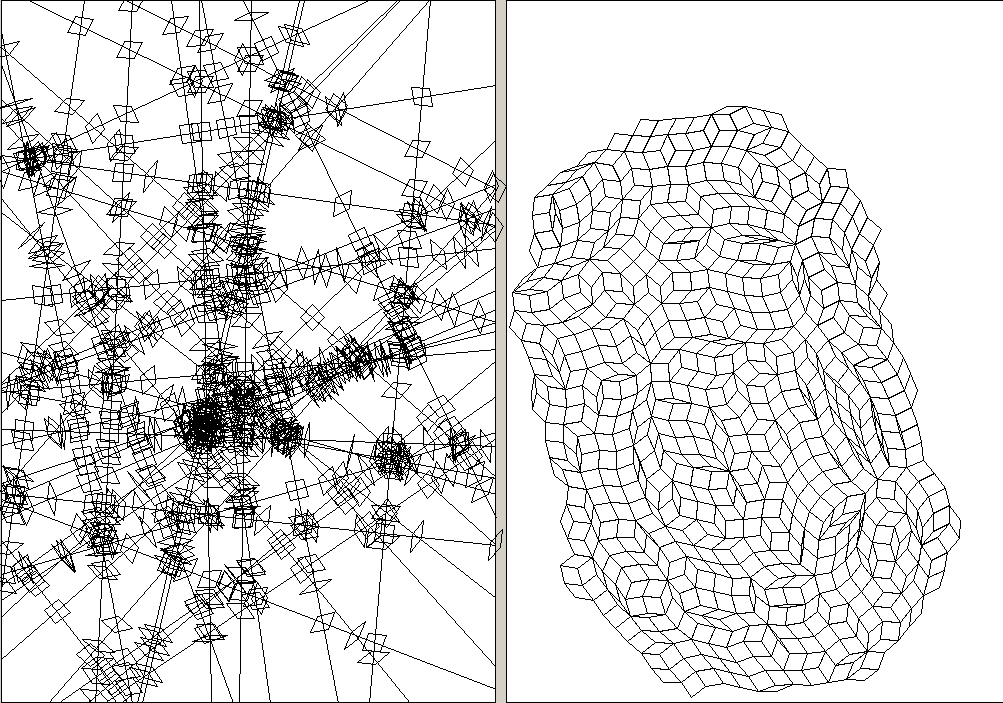
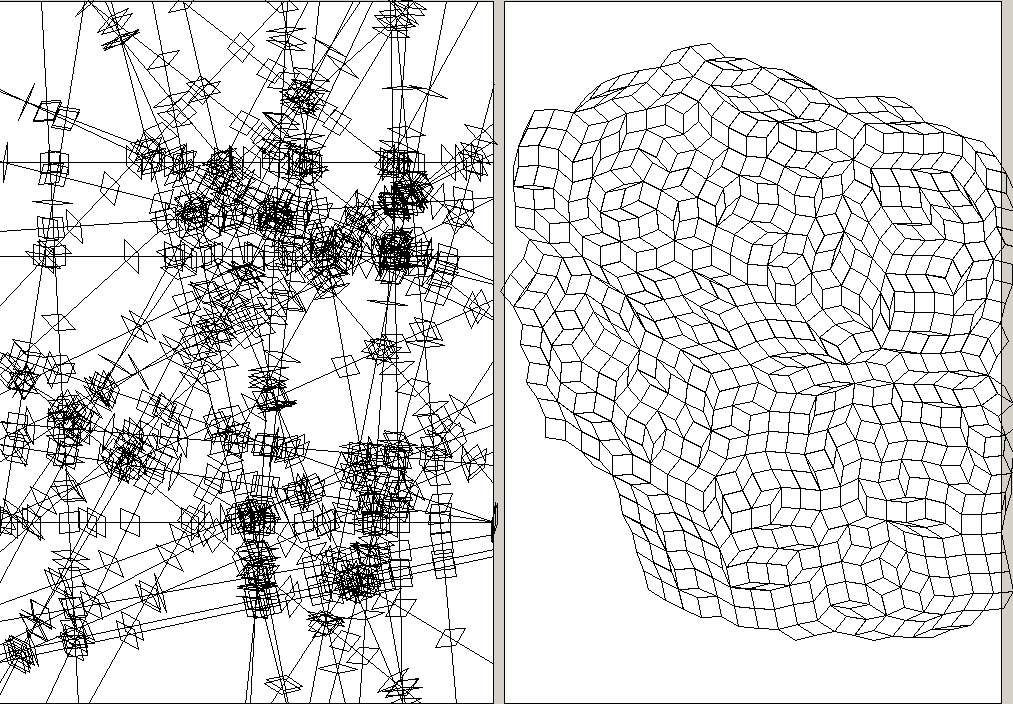
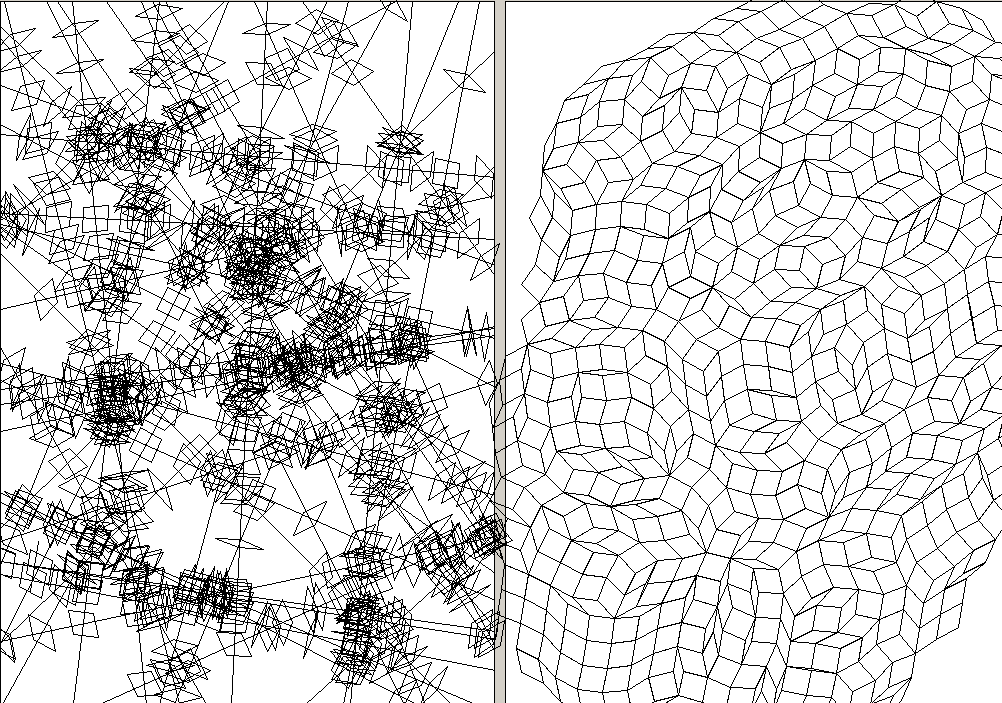
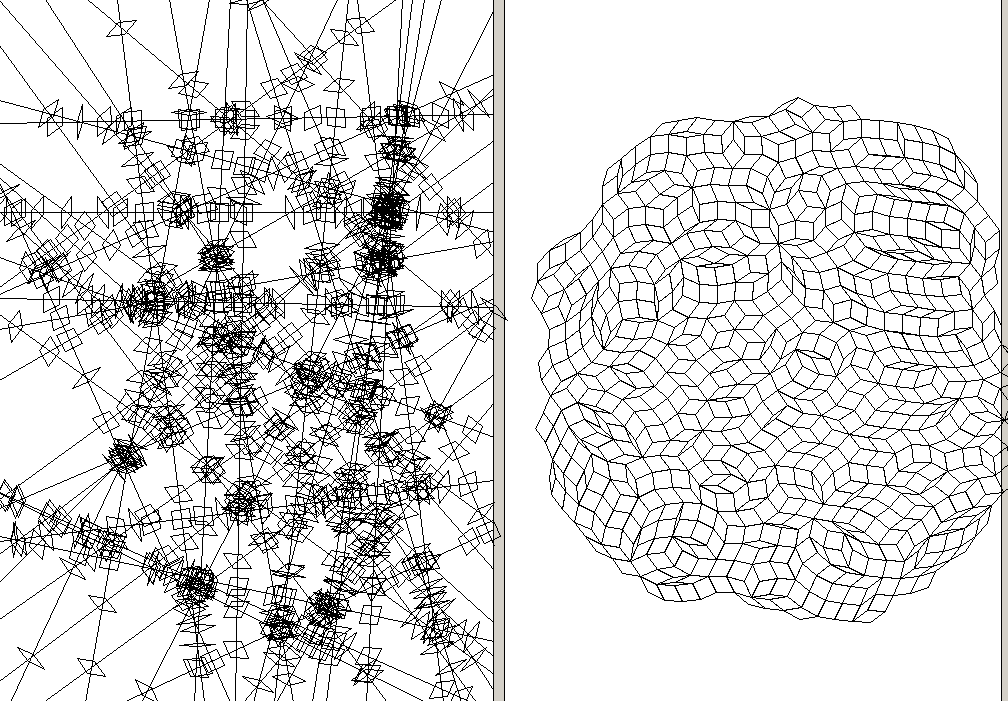
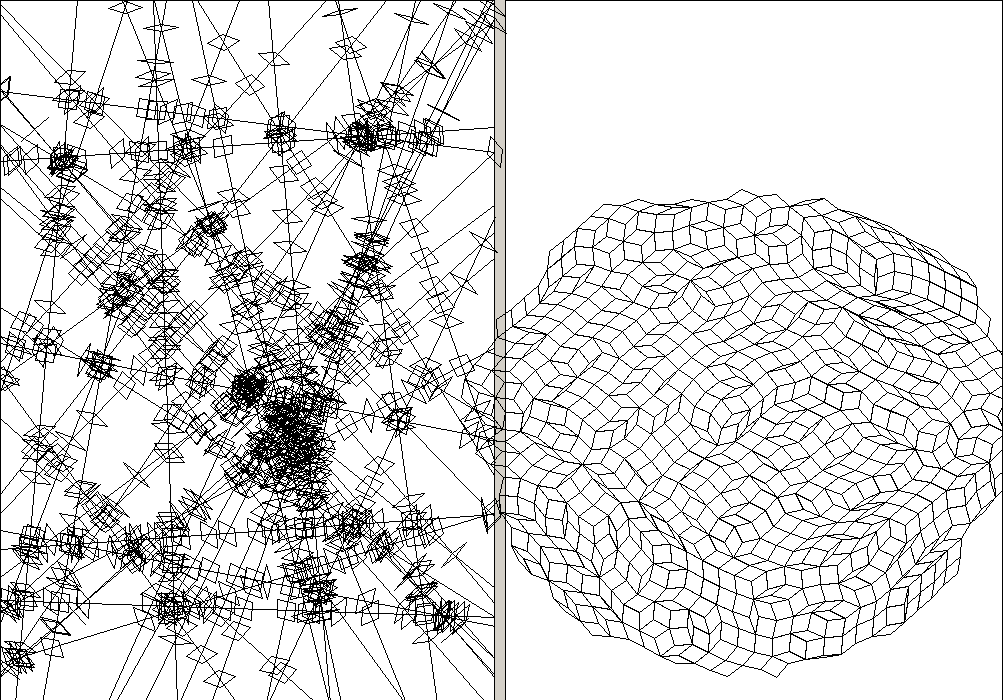
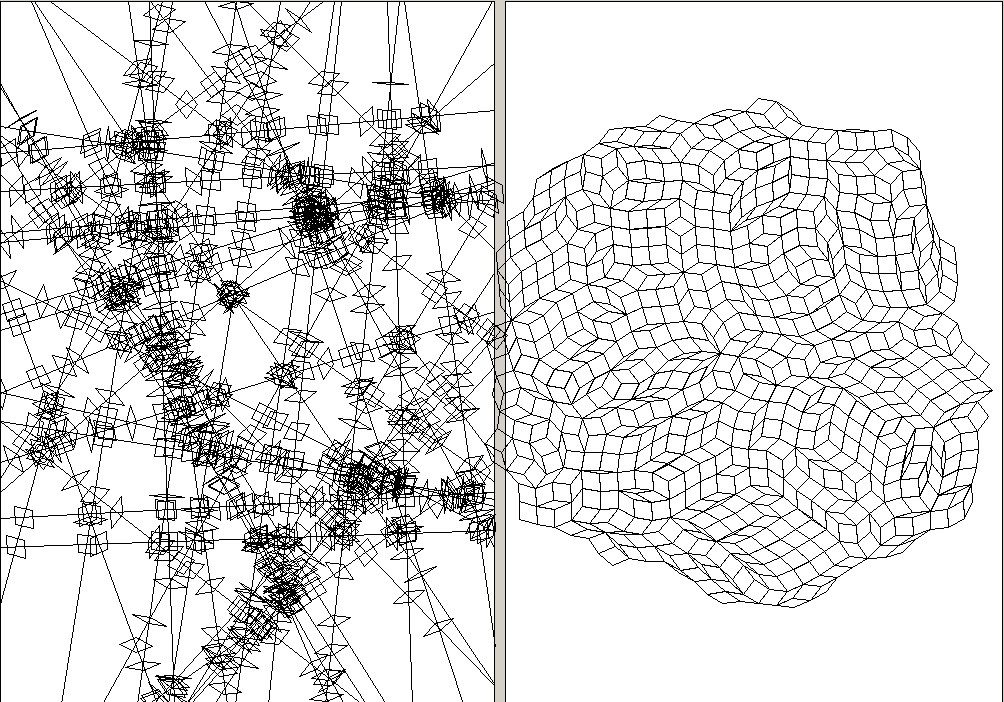
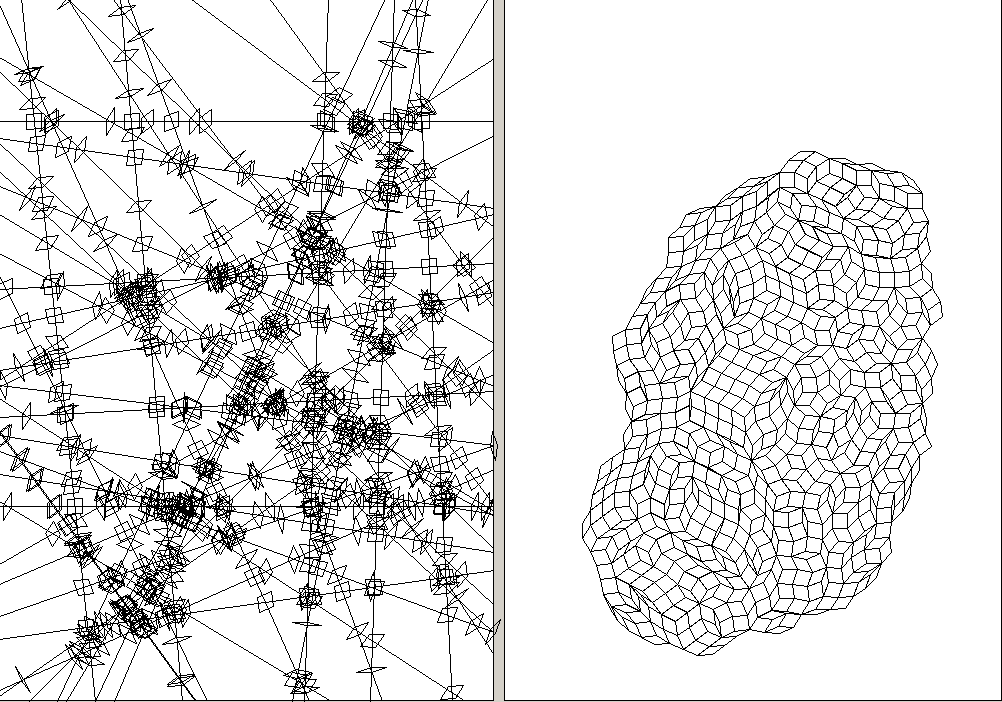
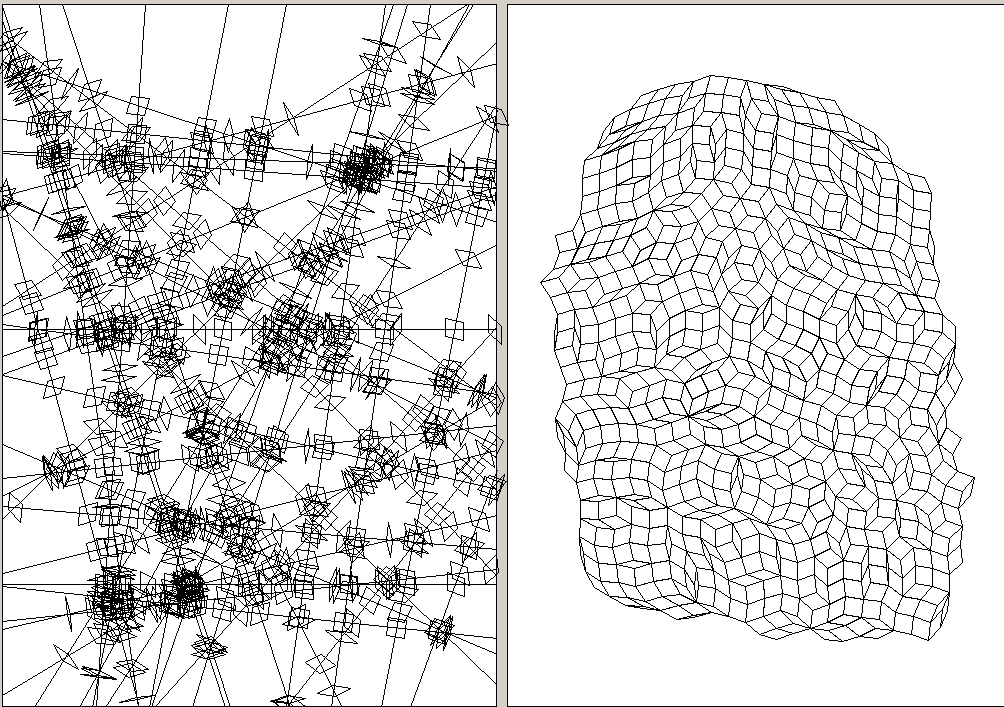
80 random lines

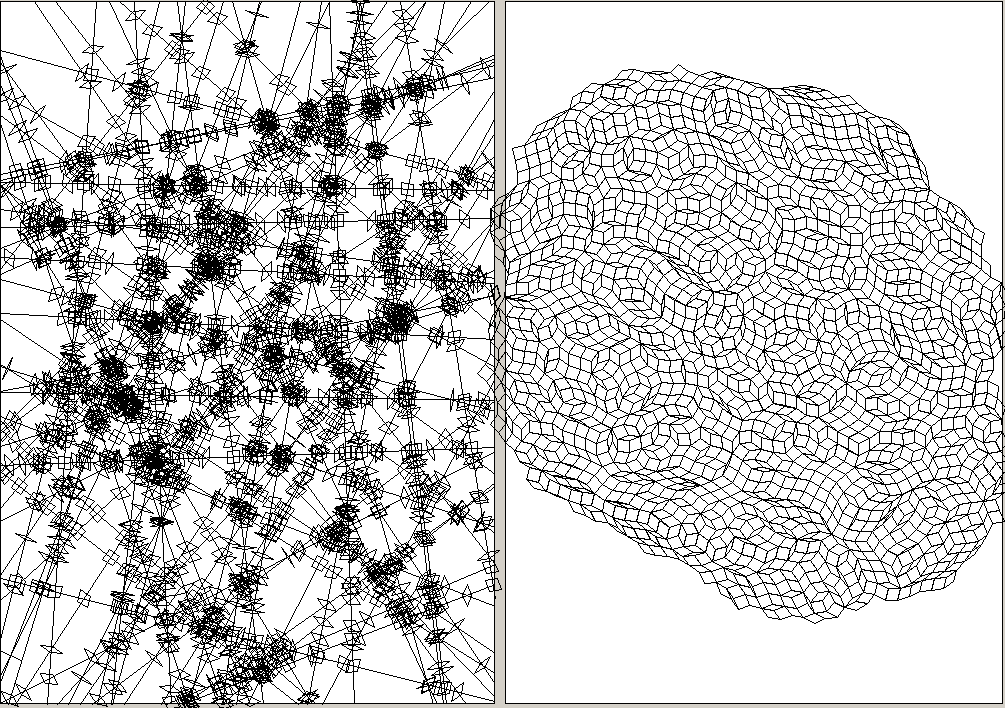
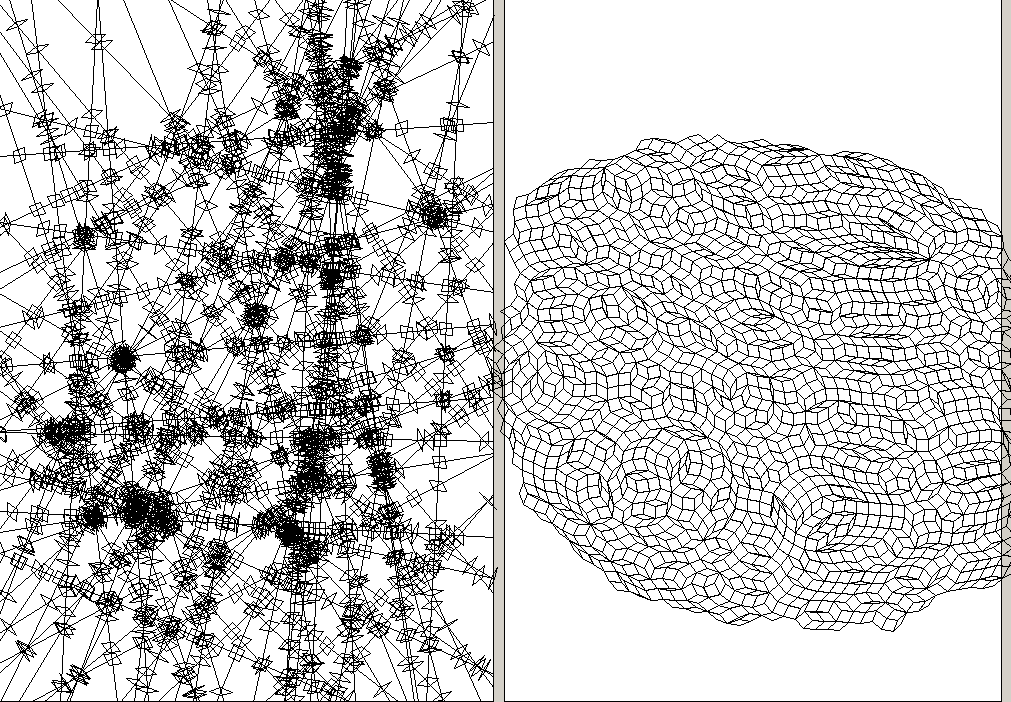
others

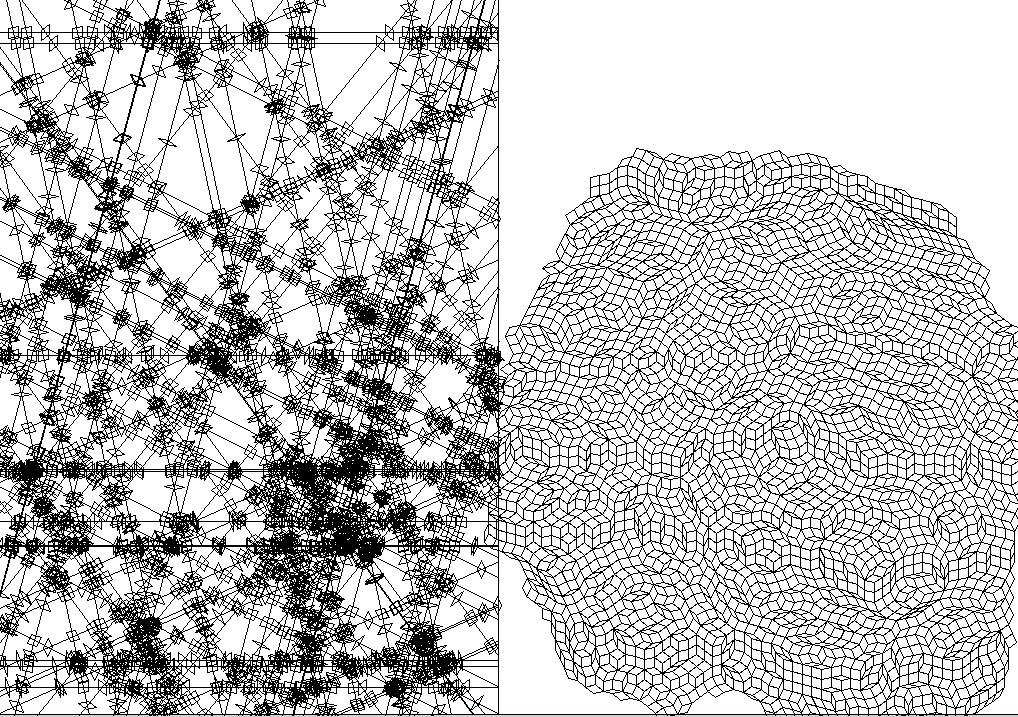
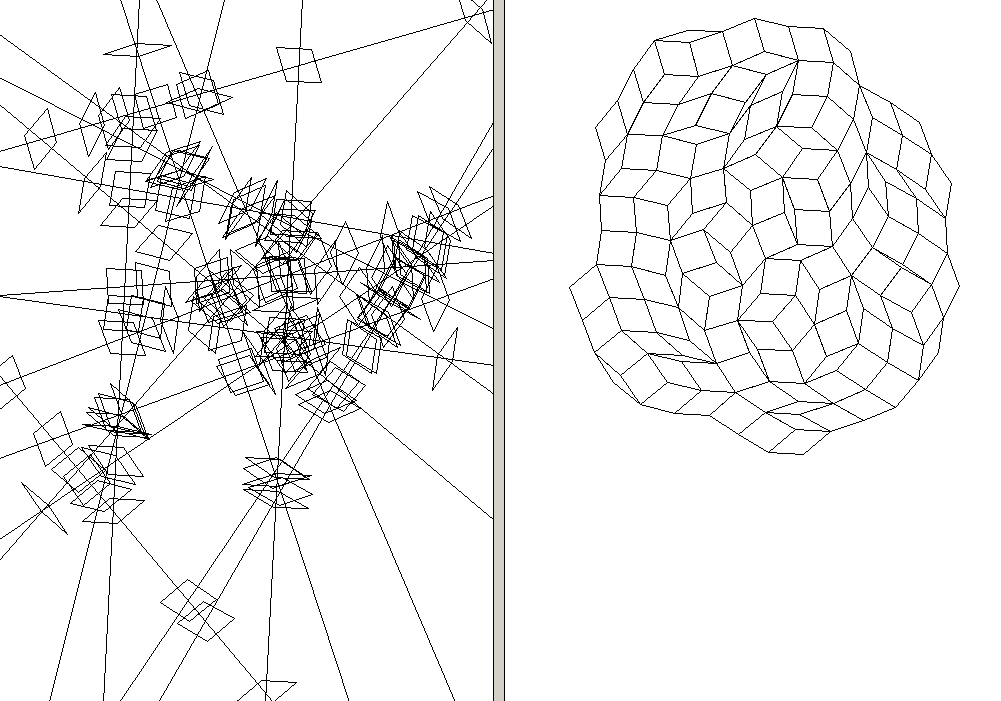
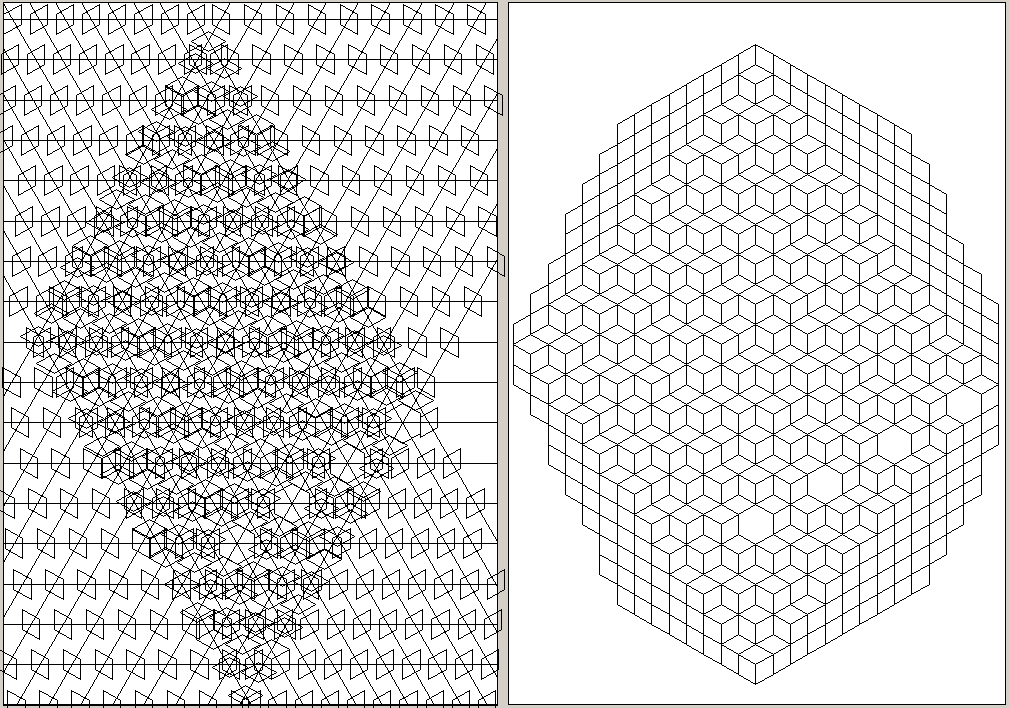
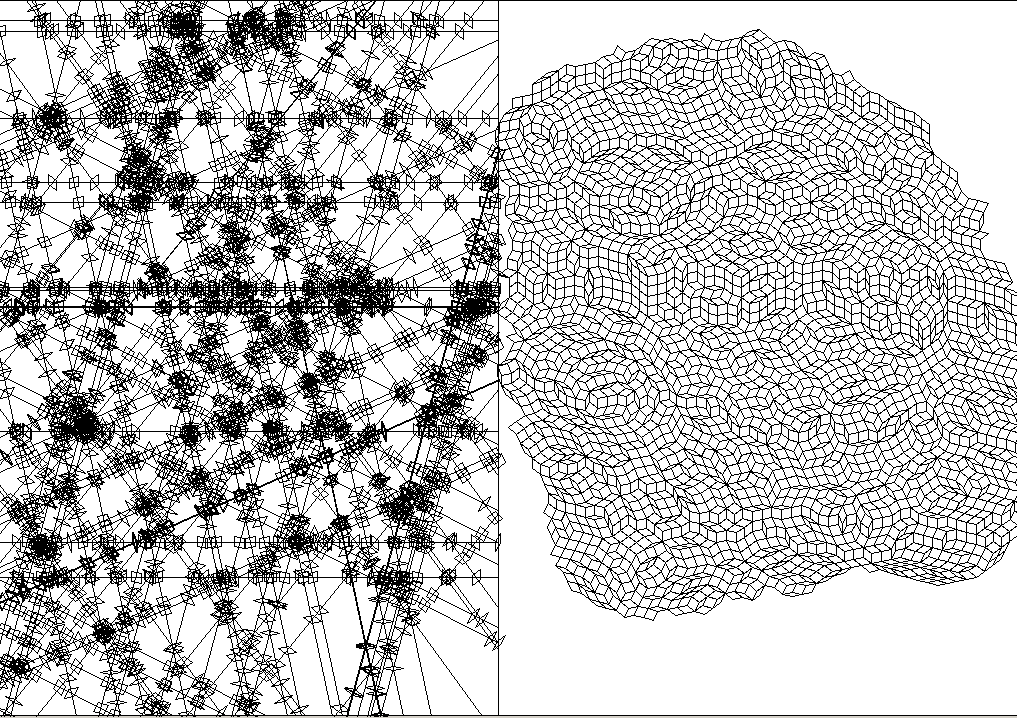
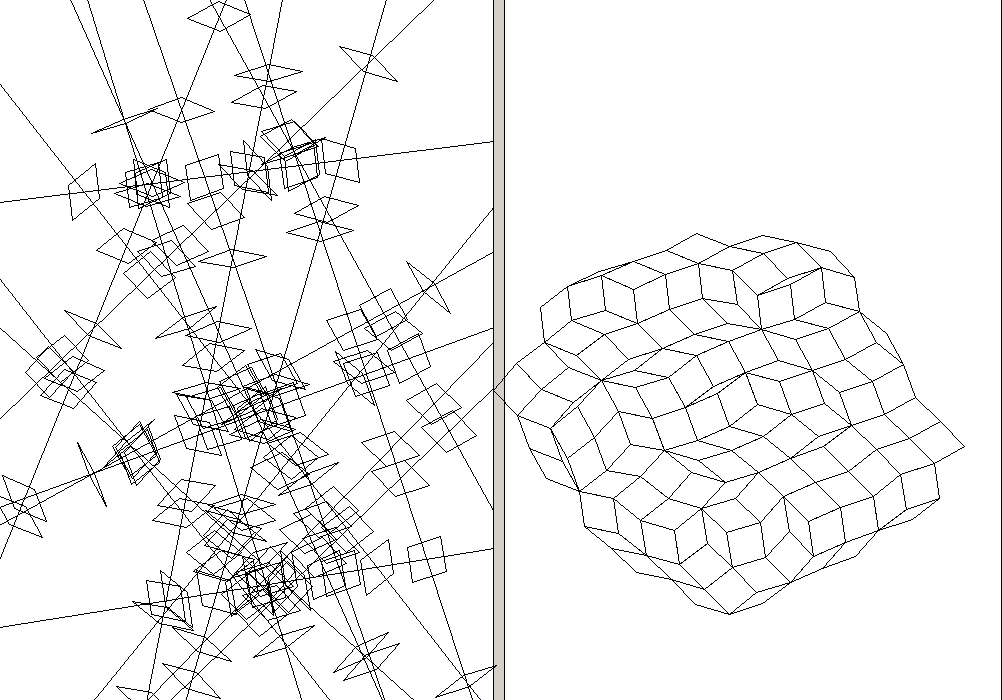
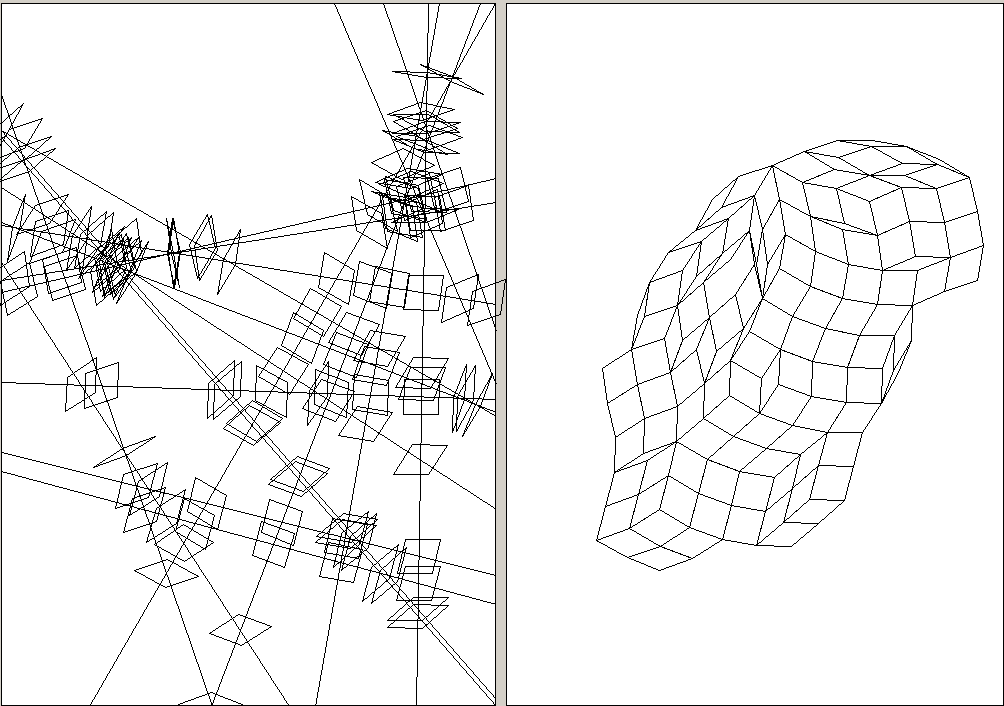
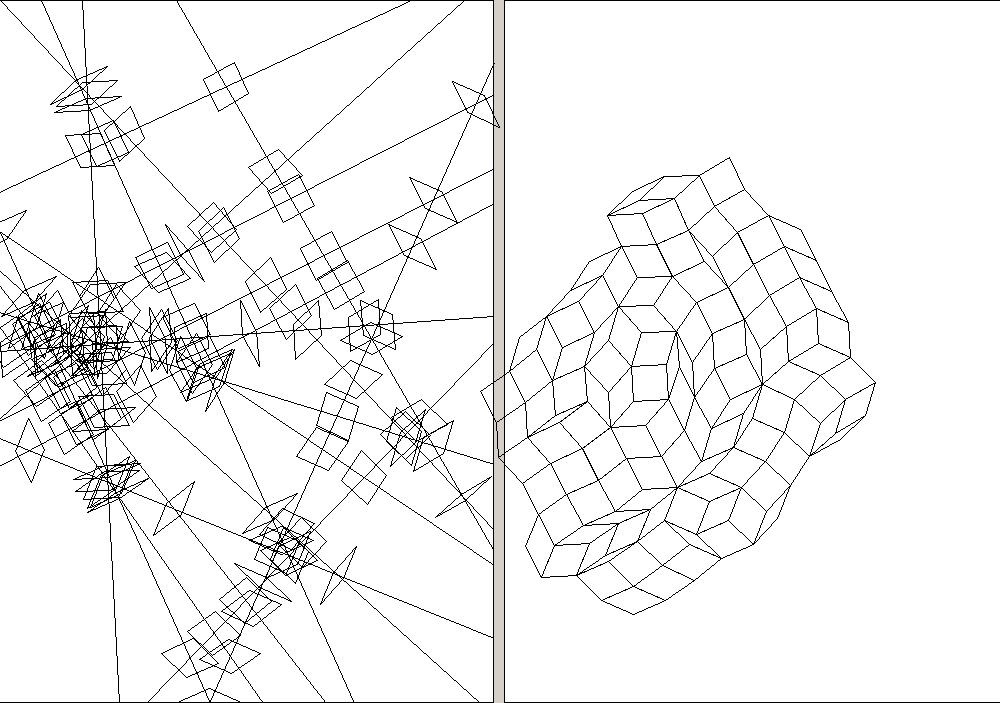
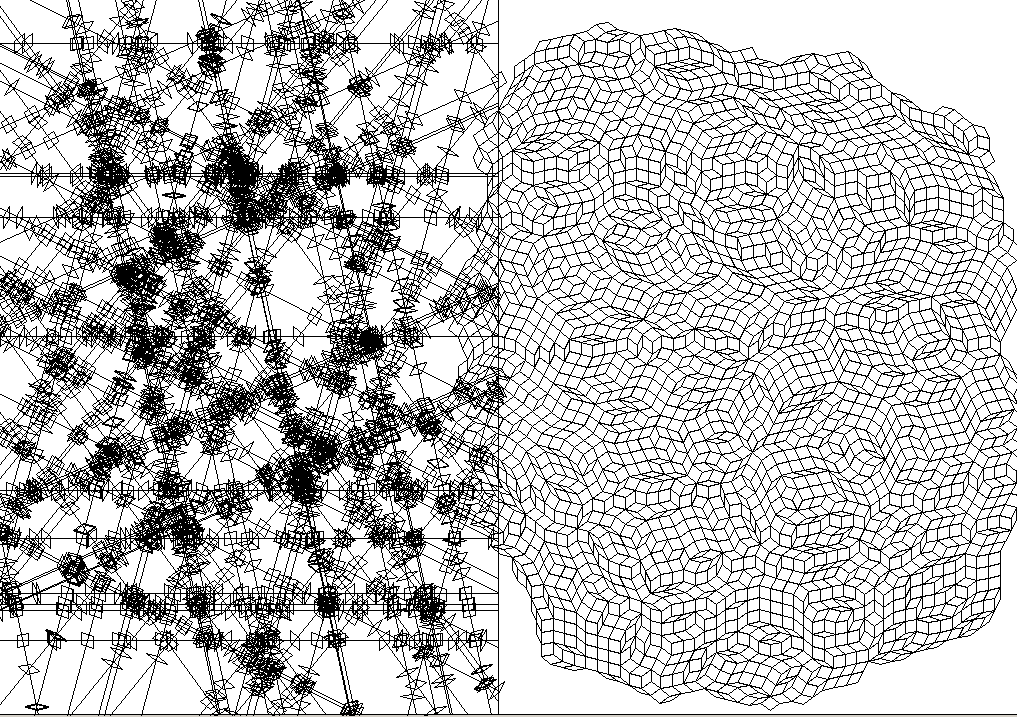
7-fold with shapes planted (i.e. lines meeting at a point)

decagon planted in centre

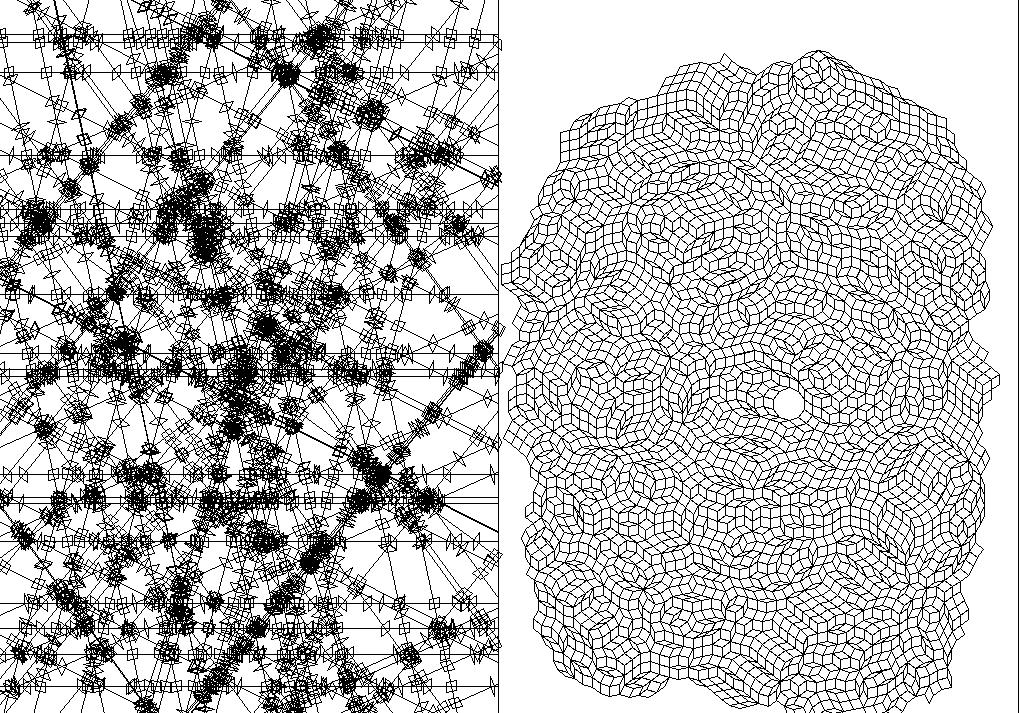
6-gon planted

8-gon planted

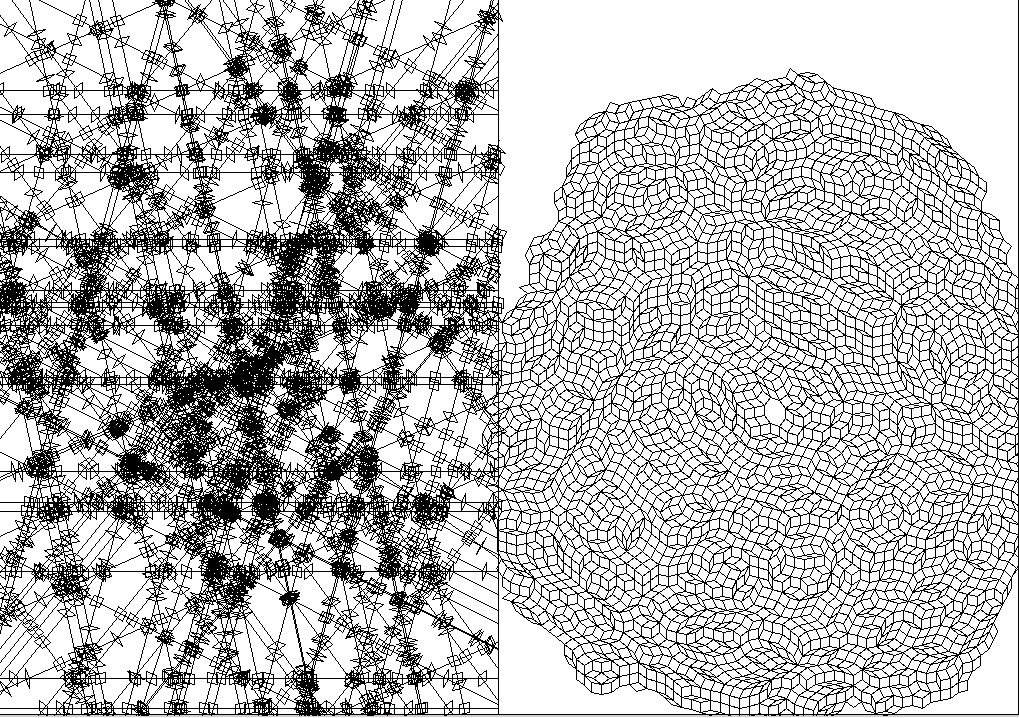
face

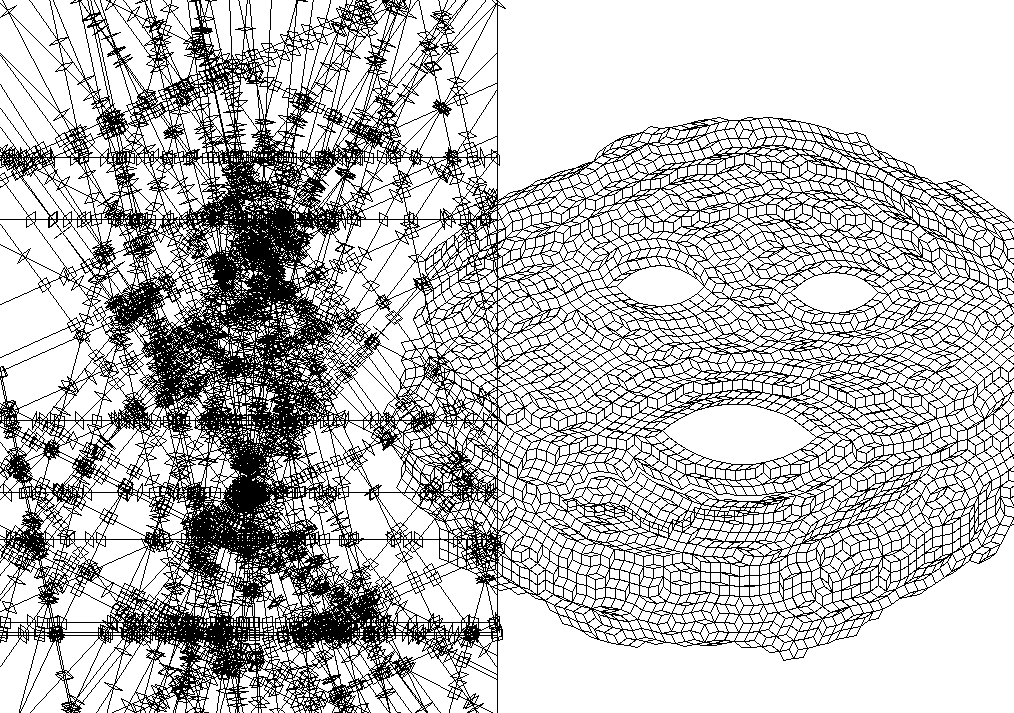
[Dec 2015]